The Energy of Flowing Air
3 min read
The Origin of Wind Energy
A windsock is used at airfields and roads to determine the approximate direction and strength of the wind.
The origin of wind energy can be found in irregular heating of the Earth’s surface by solar radiation. Low layers of air get heated by the surface and ascend due to their lower density, allowing colder air masses to move in. Pressure highs and lows develop and as the pressure between these tries to equalize, wind starts blowing.
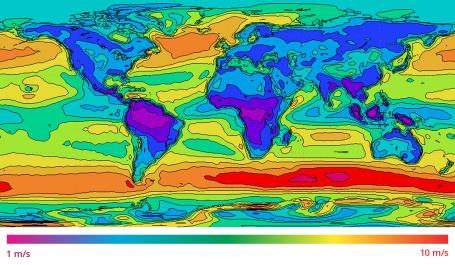
Parameters Influencing the Wind Energy Utilization
From an energetic point of view, this is an opportunity to capture the kinetic energy of the flowing air using a wind turbine. The most important factor for harnessing wind energy is the speed of the wind. The energy of a moving air mass is directly proportional to the area through which the air is flowing times its speed squared. The power flowing through a unit area is directly proportional to the air density and the wind speed to the third power. From this we can deduce that when the wind speed doubles, power production can increase by a factor of up to eight. Most wind turbines however, reach their maximum output at a speed of 15 m/s (30 knots) for which they are designed and the output does not grow with further increase in wind speed. Therefore, wind turbines should only be built at places with relatively high mean wind velocities.
The wind loses only a part of its energy to the blades of a turbine. The theoretical maximum efficiency of a wind turbine was defined in a theory by Albert Betz in 1920 and lies at 59.26%. This optimum state is reached when the air mass flowing through the turbine loses about one third of its speed. The real efficiency of wind turbines is, of course, lower and is determined by the design of the turbine, friction, angle of attack settings and other factors.
Aside from the efficiency of a wind turbine, another important parameter of its performance is the annual coefficient of utilization which shows the ratio between the actual and the theoretically achievable annual output. Usually it is about 20%.
The power output of a wind engine can be determined using the following formula:
Pm = 0,125 × Cp × ρ × v3 × π × D2
where:
| Pm | useful power (W) |
| Cp | power coefficient (efficiency) |
| ρ | air density (kg/m3) |
| v | wind speed (m/s) |
| D | propeller diameter (m) |